【基礎編】第5回：回帰分析の基礎

回帰分析の目的と種類

回帰分析の主な目的は、ある変数（目的変数）と他の一つまたは複数の変数（説明変数）との関係を明らかにし、その関係性を数式化することです。これにより、説明変数の値から目的変数の予測や、各説明変数が目的変数に及ぼす影響の評価が可能となります。

​これにより、説明変数の値から目的変数の予測や、各説明変数が目的変数に及ぼす影響の評価が可能となります。

​回帰分析は、説明変数の数やデータの特性に応じて以下のように分類されます。

単回帰分析	一つの説明変数を用いる場合
重回帰分析	複数の説明変数を用いる場合
ロジスティック回帰分析	目的変数が二値（例：疾患の有無）の場合に用いる手法

単回帰分析のモデル構築と解釈

単回帰分析では、目的変数\(Y\) と一つの説明変数\(X\)の関係を以下の線形モデルで表します。

\(Y=\beta_0+\beta_1X+\varepsilon\)

ここで：

• \(\beta_0\)：切片（Y軸との交点）
• \(\beta_1\)：回帰係数（傾き）
• \(\varepsilon\)：誤差項

このモデルを構築する際、最小二乗法を用いて\(\beta_0\)と\(\beta_1\)を推定します。最小二乗法は、観測値とモデルによる予測値の差の二乗和を最小化する方法です。

解釈

• 切片(\(\beta_0\))：説明変数(\(X\))が0のときの目的変数(\(Y\))の予測値を示します。
• 回帰係数(\(\beta_1\))：説明変数(\(X\))が1単位増加したときに、目的変数(\(Y\))が平均してどれだけ変化するかを示します。

単回帰分析の医療シナリオと解析

シナリオ

ある病院で血圧と年齢の関係を調査しています。年齢が高くなるほど血圧も高くなるのかを検討します。

データセット説明（架空）

• 年齢（30〜70歳）
• 収縮期血圧(mmHg)

Pythonコード（単回帰分析）

 

結果の解釈

 

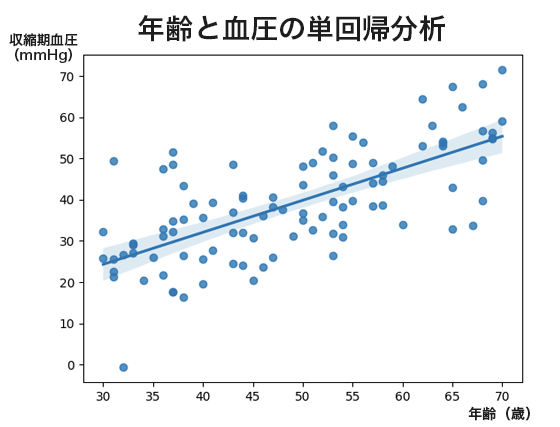
単回帰分析の結果から、年齢が増えるごとに平均して血圧が上昇することが分かります。グラフ上の直線はその関係を視覚的に示しています。個人差はありますが、年齢と血圧の関連性が分かります。

重回帰分析のモデル構築と解釈

重回帰分析では、目的変数\(Y\)と複数の説明変数\(X_1,X_2,\dots,Xp​\)の関係を以下の線形モデルで表します：

\(Y=\beta_0+\beta_1X_1+\beta_2X_2+\dots+\beta_pX_p+\varepsilon\)

• \(\beta_0\)​：切片
• \(\beta_1,\beta_2,\dots,\beta_p\)​：​各説明変数の回帰係数​
• \(\varepsilon\)：誤差項

最小二乗法を用いて、各回帰係数を推定します。

解釈

• 回帰係数 (\(\beta_i\)​)：他の説明変数が一定のとき、説明変数(\(X_i\))が1単位増加すると、目的変数(\(Y\))が平均して(\(\beta_i\))だけ変化することを示します。​
• 決定係数(\(R^2\))：モデルが目的変数の変動をどれだけ説明しているかを示す指標で、1に近いほどモデルの適合度が高いことを意味します。​

重回帰分析の医療シナリオと解析

シナリオ

​ある病院で、患者の収縮期血圧（mmHg）を、年齢（歳）、BMI（Body Mass Index）、喫煙の有無（1：喫煙者、0：非喫煙者）を用いて予測してみましょう。​

データセット説明（架空）

• 年齢（30〜70歳）
• BMI(18.5〜35​)
• 喫煙(0または1​)
• 収縮期血圧(100〜180 mmHg​)

Pythonコード（重回帰分析）

 

重回帰分析の詳細な解釈

 

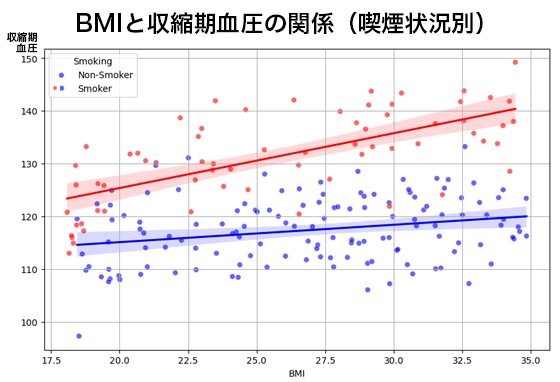
1. 回帰係数（Coefficient）

定数項（const: 85.848530）	モデルにおける切片は、すべての説明変数（Age、BMI、Smoking）の値が0の場合のSBPの予測値です。 実際の疫学研究では、年齢やBMIが0という状況は現実的ではないため、直接の臨床解釈は難しいですが、モデル全体の基準値として理解されます。
Age（0.294927）	年齢が1歳上昇するごとに、他の要因（BMIと喫煙状態）が一定であると仮定した場合、SBPが平均して約0.29 mmHg増加することを意味します。この効果は、加齢に伴う生物学的変化を反映していると考えられます。
BMI（0.630887）	BMIが1単位上昇すると、他の変数が一定の場合、SBPが平均して約0.63 mmHg増加することを示します。BMIの上昇は体重過多や肥満に関連しており、これが血圧上昇のリスク因子である可能性を示唆しています。
Smoking（14.797348）	喫煙者（Smoking=1）の場合、非喫煙者（Smoking=0）に比べて、SBPが平均して約14.80 mmHg高いことを示しています。これは、喫煙が血圧に強い影響を与えることを反映しています。

2. 標準誤差（Std Error）

標準誤差は、各回帰係数の推定値のばらつき（推定の不確実性）を示します。数値が小さいほど、係数の推定精度が高いことを意味します。

例として、Ageの標準誤差は0.031891であり、これは推定された年齢効果の精度が高いことを示唆しています。同様に、BMI（0.075975）およびSmoking（0.802550）の標準誤差も、それぞれの効果推定が比較的精確であることを表しています。

3. t値（t Statistic）

t値は、各回帰係数がその標準誤差に対してどれほど大きいかを示す指標です。大きな絶対値のt値は、該当する変数の効果が統計的に有意である可能性が高いことを意味します。

• Ageのt値：9.247838
• BMIのt値：8.303896
• Smokingのt値：18.437923

これらはすべて、各変数がSBPに対して強い独立した影響を持っていると解釈できます。特にSmokingのt値は非常に高く、喫煙が血圧上昇に対して非常に強い影響を与えていることが示唆されます。

4. p値（P>|t|）

p値は、各変数の効果が偶然の産物である可能性を評価するための指標です。一般に、p値が0.05未満であれば、その効果は統計的に有意差があると判断されます。

• Ageのp値：3.961806e-17
• BMIのp値：1.628594e-14
• Smokingのp値：1.094499e-44

これらの極めて低いp値は、各変数がSBPに与える影響が偶然ではなく、実際に統計的に有意であると結論づけられる根拠となります。また、定数項のp値も非常に低い（2.226460e-80）ため、モデル全体としても強固な統計的有意性が確認されます。

重回帰分析のまとめ

この重回帰モデルにおいて、年齢、BMI、そして喫煙状態はすべて、収縮期血圧（SBP）に対して統計的に有意な影響を与えていると解釈されます。

各係数は、他の変数を制御した上での独立した効果を示しており、特に喫煙は血圧に対して強い上昇効果を持つことが示唆されています。

ロジスティック回帰分析のモデル構築と解釈

ロジスティック回帰分析は、目的変数が二値（例：疾患の有無、成功・失敗など）の場合に、複数の説明変数との関係を解析し、その発生確率を予測するための統計手法です。

これは、線形回帰分析では適切にモデル化できない二値アウトカムに対して有用です。

モデルの構築

ロジスティック回帰モデルは、以下の数式で表されます：

$$logit(P)=\ln\left( \frac{P}{1-P} \right)=\beta_0+\beta_1X_1+\beta_2X_2+\cdots+\beta_pX_p$$

ここで：

• \(P\)：目的変数が1（例：疾患あり）となる確率
• \(\beta_0\)：切片
• \(\beta_1,\beta_2,\cdots,\beta_p\)：各説明変数\(X_1,X_2,\cdots,X_p\)の回帰係数

説明変数の線形結合を用いて、目的変数が特定の状態になる対数オッズを予測します。オッズとは、ある事象が起こる確率を起こらない確率で割ったものです。

解釈

オッズ比（Odds Ratio）	回帰係数(\(\beta_i\))の指数関数(\(e^{ \beta_i }\))は、説明変数(\(X_i\))が1単位増加したときのオッズ比を示します。オッズ比が1より大きければ、目的変数が1になる確率が増加し、1より小さければ減少します。
切片(\(\beta_0\))	すべての説明変数が0のときの対数オッズを示しますが、実際の解釈は難しい場合が多いです。

Pythonコード（ロジスティック回帰分析）

   

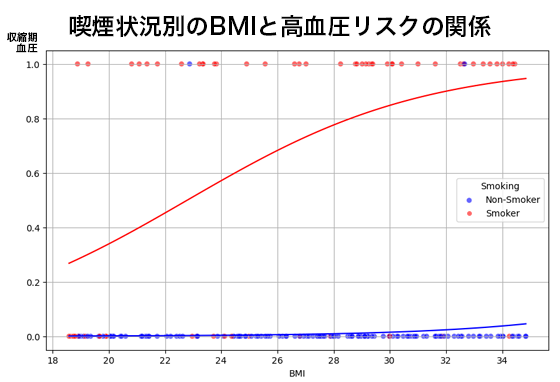
1.回帰係数 (coef)

定数項 (const: -14.4029)	定数項は、すべての説明変数（Age、 BMI）が0の場合の高血圧発症の対数オッズを表します。実際には年齢やBMIが0となることは現実的ではないため、臨床的解釈は難しいですが、モデル全体の基準値として利用されます。
Age (0.0619)	年齢が1歳増加するごとに、高血圧発症の対数オッズが0.0619増加することを示しています。対数オッズをオッズ比に変換すると、exp(0.0619) ≒ 1.064となり、1歳上昇するごとに高血圧のオッズが約6.4%上昇することが示唆されます。
BMI (0.2385)	BMIが1単位上昇すると、高血圧発症の対数オッズが0.2385増加します。これは、exp(0.2385) ≒ 1.269 に相当し、BMIが1単位増えるごとに高血圧のオッズが約27%増加することを意味します。体重過多や肥満が血圧に及ぼす影響を反映している可能性を示唆します。
Smoking (5.9112)	喫煙している場合（Smoking=1）、非喫煙者（Smoking=0）に比べて高血圧発症の対数オッズが5.9112上昇することを示します。 これをオッズ比に変換すると、exp(5.9112) ≒ 367となり、喫煙が高血圧のリスクに極めて大きな影響を及ぼすことが示されています（ただし、この大きな効果はシミュレーションデザインの結果であり、実際の疫学研究では通常、これほど極端な値にはならないことに留意が必要です）。

2.標準誤差 (std err)

標準誤差は、各回帰係数の推定値のばらつき（すなわち、推定の不確実性）を表します。値が小さいほど、サンプル内での変動が小さく、係数推定の精度が高いことを意味します。

例えばAgeの標準誤差0.024やBMIの0.065、Smokingの0.902は、それぞれの係数の推定精度を示しており、これらの値から各効果の推定が比較的安定していると判断できます。

3.z値 (z)

z値は、各回帰係数がその標準誤差に対してどれだけ大きいかを示す指標で、係数 ÷ 標準誤差として算出されます。

Age (z = 2.544)	年齢の効果が0からどれほど逸脱しているかを示しており、z値が約2.54であるため、年齢が高血圧リスクに与える影響は統計的に有意である可能性が高いと解釈されます。
BMI (z = 3.648)	BMIのz値は約3.65で、これも高い統計的有意性を示唆しています。
Smoking (z = 6.554)	喫煙のz値は約6.55と非常に大きく、喫煙が高血圧発症に与える影響が非常に強固であることを示しています。

z値が一般的な臨界値（例えば、±1.96）を超えている場合、帰無仮説（係数が0であるという仮説）は棄却されるため、各変数の効果が統計的に有意であると判断されます。

4.p値 (P>|z|)

p値は、帰無仮説（ここでは、各説明変数が高血圧発症に影響を与えない＝係数が0である）の下で、観測されたz値以上の極端な値が得られる確率を示します。

Age (p = 0.011)	p値が0.011であり、通常の有意水準0.05未満であるため、年齢の効果は統計的に有意と判断されます。
BMI (p = 0.000)	BMIのp値は非常に小さく、BMIが高血圧のリスク因子として強く寄与していることが示されています。
Smoking (p = 0.000)	喫煙のp値も非常に低く、喫煙が高血圧の発症リスクに対して有意な影響を持つと結論づけられます。

p値が0.05未満である場合、観察された効果は偶然の産物である可能性が低く、統計的に有意であるとされます。

ロジスティック回帰分析のまとめ

このロジスティック回帰モデルでは、年齢、BMI、喫煙の各変数が高血圧発症のリスクに対して統計的に有意な影響を与えていることが示されています。

Age	1歳増加するごとに高血圧のオッズが約6.4%上昇。
BMI	1単位増加するごとにオッズが約27%上昇。
Smoking	喫煙者は非喫煙者に比べ、非常に大きく高血圧のリスクが増加（オッズ比約367）している。

これらの結果は、各要因が高血圧の発症において独立してリスクを高めることを示しており、疫学的リスク評価や予防介入の立案において重要な示唆を提供します。

基礎シリーズのまとめ

これまでの基礎シリーズを通じて、統計学の基本的な概念と手法について解説しました。

これらの知識は、臨床研究の設計やデータ解析を行う上での土台となります。統計学的手法を適切に理解し活用することで、データから有益な情報を引き出すことができます。

ぜひ論文の解釈や臨床にもご活用ください。​​