【応用編】第1回：多変量解析入門

多変量解析が必要な理由（交絡の理解）

多変量解析とは、文字通り複数（多変量）の要因を同時に取り扱う解析手法のことです。

臨床の現場や医学研究において、私たちが注目するアウトカム（結果）は、多くの場合、一つの要因だけで説明できるほど単純ではありません。たとえば、高血圧や糖尿病といった生活習慣病の発症リスクは、年齢や性別、食生活、運動習慣など、さまざまな要素が絡み合っています。

これらを無視して単一の要素だけで分析を行うと、本当に影響を及ぼしている要因が見えなくなったり、間違った結論に至ったりしてしまいます。このような現象を「交絡（こうらく、confounding）」と呼びます。

以前、友人が参加した生活習慣と循環器疾患リスクの関連を調べる研究で、こんなことがありました。
初期の単変量解析で「コーヒーを1日2杯以上飲む人は、心血管疾患の発症率が有意に低い」という結果が出てきたのです。p値は0.02、オッズ比は0.68と、かなり説得力がありそうに見えました。しかし、これは間違いでした。

というのも、コーヒーをよく飲む人には「都会的なライフスタイル」や「職業的ストレスは多いが健康意識も高い」といった背景がある可能性が高いです。特に友人の調査では、コーヒー摂取量が多い群では、定期的に運動をしている人の割合が明らかに高かったのです（週3回以上の運動実施者：コーヒー高摂取群で72%、低摂取群で51%、p<0.01）。

そこで、多変量ロジスティック回帰分析(これは広い意味での重回帰分析ですが、別物と考えたほうがいいかもしれません)という解析を行い、運動習慣、年齢、性別、喫煙歴、飲酒頻度などをすべてモデルに投入して調整を行いました。するとどうでしょう、コーヒー摂取のオッズ比は0.68から0.91に上昇し、95%信頼区間は0.75〜1.10、p値は0.32となり、有意差は消えてしまったのです。

このように、交絡因子を調整することはとても重要です。単純な相関関係では一見よさそうに見える結果でも、それが他の要因によって「見かけ上」つくられた関係である可能性は常にあるのです。

交絡を正しく補正しないまま結果を信じてしまうと、「コーヒーをたくさん飲めば心疾患を予防できる」という誤った結果を導いてしまいます。多変量解析は、そうした誤解を避け、データの中に埋もれている「本当の因果関係」を見つけるための重要なツールなのです。

重回帰分析の復習（単回帰 → 重回帰）

単回帰分析では、ひとつの説明変数と目的変数の関係を見ていました。たとえば「BMIが血圧に与える影響」といった一対一の関係です。

重回帰分析では、複数の説明変数（例：BMI、年齢、性別、喫煙歴など）を同時にモデルに入れて、目的変数（例：血圧）に対するそれぞれの影響を評価します。これにより、交絡因子の影響を除外した、純粋な効果が見えてきます。

偏回帰係数の実践的な解釈方法

重回帰分析の出力結果には、それぞれの説明変数に対応する「偏回帰係数（partial regression coefficient）」が含まれています。これは「他のすべての説明変数の影響を一定にしたときに、その変数が目的変数にどれだけ影響するか」を示す指標です。

例えば、BMIの偏回帰係数が0.8であれば、「年齢や性別などが一定のとき、BMIが1増加すると血圧が平均0.8mmHg上昇する」という意味になります。

以下の3点は、セットで解釈するようにするとよいでしょう：

• 偏回帰係数（効果の方向と大きさ）
• 95%信頼区間（推定の不確実性）
• p値（統計的有意性）

モデルの診断と前提条件のチェック

重回帰分析を行うとき、以下の前提条件が満たされている必要があります：

• 1.線形性：説明変数と目的変数の関係が直線的である
• 2.正規性：残差（予測値と実測値の差）が正規分布に従う
• 3.等分散性：残差の分散が説明変数の値によらず一定である

これらの条件が崩れていると、推定値の信頼性が下がってしまいます。これらの前提条件が満たされているかどうかを判断するためには、残差プロットやQ-Qプロットを描画してみることが有効です。

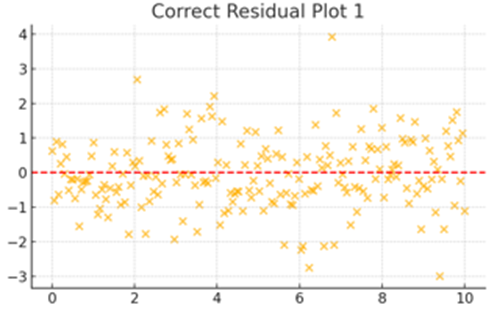
これは前提条件が満たされている場合の残差プロットの例です。点がランダムに散らばっていますね。

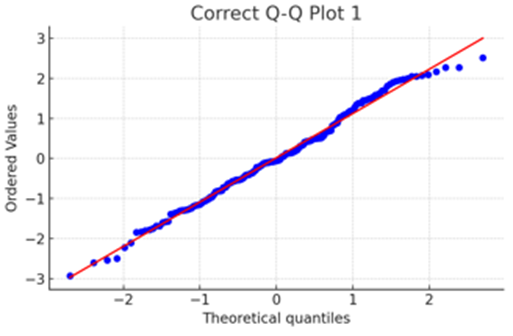
これは正規分布しているデータのQ-Qプロットです。点がきれいに対角線上に乗っているので、データは正規分布していると考えて良さそうです。

次に、重回帰分析の条件にあわない残差プロットを3つ提示します。

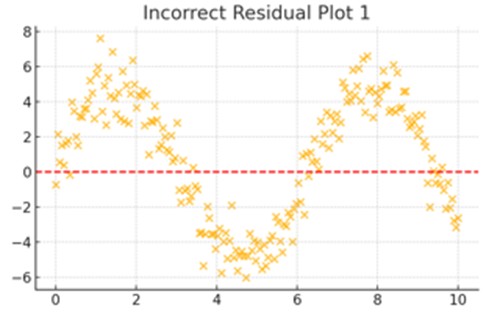
これは曲線的なパターンを示しており、線形性がないデータであると推測されます。

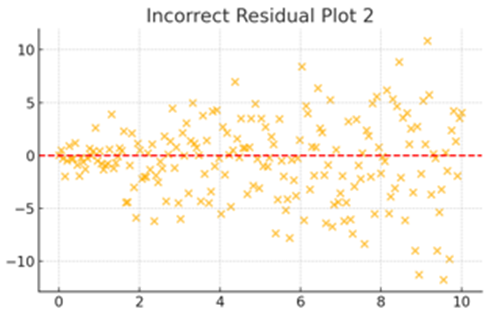
これはX軸が右に行くにつれてラッパ型に残差が広がっています。この残差は分散が不均一(等分散ではない)と推測されます。

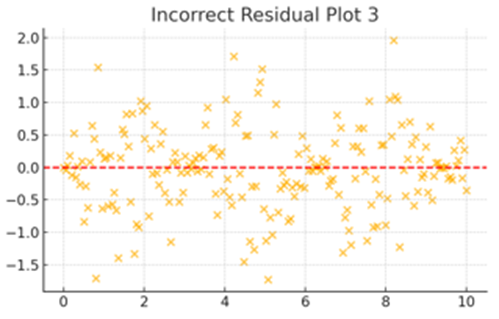
これはぱっと見た感じ、少しわかりにくいかもしれませんが、残差が周期的に0に収束しており、なにかの規則性を持っているようです。

次に、重回帰分析の条件にあわないQ-Qプロットを2つ提示します。

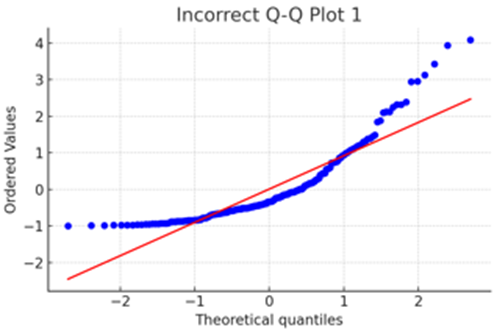
データが指数分布している場合はこのようなQ-Qプロットになります。

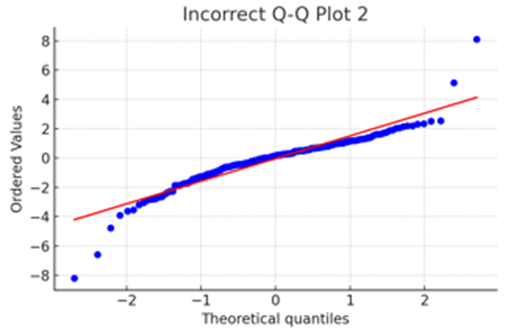
データがt分布している場合はこのように裾が上(または下)に大きくカーブしたQ-Qプロットになります。

(注)今回は触れませんが、 t分布しているデータを重回帰分析に用いるべきではないかというと、必ずしもそうではありません。

変数選択のポイント

重回帰分析では、「説明変数は多ければ多いほど良い」というわけではありません。変数を安易に増やしすぎると、訓練データにはよく適合するものの、未知のデータには適応できない過適合（overfitting）が起こりやすくなります。

基本方針

以下の2つの観点から変数選択を行うことが重要です。

【1】臨床的な意義

疾患やアウトカムとの関連が強いとされる変数（例：年齢、性別、既往歴など）は、統計的に有意でなくても含めるべき場合があります。

目的変数の背景病態と照らし合わせて、「この因子は含めるべきだ」と判断できる変数は慎重に扱います。

【2】統計的な基準

• p値：通常、p < 0.05であれば統計的に有意とされます。
  ただし、有意でなくても臨床的に意味があれば残す判断もあります。
• AIC（赤池情報量基準）：モデルの良さと複雑さのバランスを見る指標。
  数値が小さいほど良いモデルとされます。
  複数モデルを比較して、最もAICが低いモデルを選ぶ手法も一般的です。

サンプルサイズとの関係

変数の数が多いと、パラメータ推定が不安定になり、誤差が大きくなります。そのため、経験則として以下の目安が用いられます：

「1つの説明変数につき10〜15例」
150例のデータがあるなら、投入する変数は 最大10〜15個程度 に抑えるのが安全です。

より進んだ変数選択法

変数選択には自動的な方法もあります：

• ステップワイズ法（逐次選択）：変数を1つずつ追加・削除しながらモデルを評価する
• LASSO回帰：変数の重要性に応じて係数を縮小、一部をゼロにすることで変数を自動選別する

ただし、こうした方法も万能ではなく、

• 「解釈しにくいモデル」になりやすい
• 「統計的に良くても、臨床的に意味がない」変数が残ることがある

といった注意点もあります。したがって、臨床的妥当性と統計的根拠のバランスを意識することが、最も重要な原則です。

このように、変数選択は単なる「統計の作業」ではなく、「何を説明し、何を除外するか」という医学的判断の積み重ねとも言えます。

モデルはあくまで「解釈できる」ものであるべきですから、変数の選び方ひとつで、研究の信頼性が大きく左右されることを意識しておきましょう。

まとめ

今回は、重回帰分析の基礎をおさらいしながら、多変量解析における交絡の調整や偏回帰係数の読み取り方を学びました。

• 交絡因子を無視すると誤った結論に至る
• 重回帰分析は、交絡のコントロールに不可欠
• 偏回帰係数・信頼区間・p値を組み合わせて結果を読み解く
• モデル診断では線形性・正規性・等分散性をチェック
• 変数は「多すぎず・少なすぎず」臨床的意義と統計的妥当性で選択

臨床の現場では、さまざまな要因が患者さんのアウトカムに影響します。重回帰分析を使えば、それらを同時に考慮しながら交絡の影響を調整し、より「本当らしい関係」に近づくことができます。多変量解析は、そんな実践的な道具のひとつですね!

次回は「ロジスティック回帰分析」について解説します。生死・有病・転帰の有無など、二値のアウトカムを扱うときに欠かせない統計手法です。

引き続き、一緒に学んでいきましょう！