【基礎編】第2回：記述統計の基礎

代表値の計算方法と適切な使用場面

代表値とは、データの中心的な傾向を示す値であり、主に以下の3つが用いられます。

1.平均値（Mean）

平均値は、データの総和をデータの個数で割った値です。​例えば、5人の患者の血圧が120、130、125、135、140 mmHgであった場合、平均値は以下のように計算されます。

 

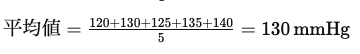
平均値は、データが正規分布に近い場合や、外れ値が少ない場合に適しています。​しかし、極端な値（外れ値）が存在すると、平均値がその影響を受けやすいため、注意が必要です。

2.中央値（Median）

中央値は、データを小さい順（または大きい順）に並べたときに中央に位置する値です。​データの個数が奇数の場合は中央の値、偶数の場合は中央の2つの値の平均を取ります。​先ほどの血圧データを例にすると、120、125、130、135、140と並べたとき、中央値は130 mmHgとなります。​

中央値は、外れ値の影響を受けにくいため、データに極端な値が含まれる場合や、分布が非対称の場合に適しています。

3.最頻値（Mode）

最頻値は、データの中で最も頻繁に出現する値です。​例えば、患者の血液型のデータでA型が最も多い場合、最頻値はA型となります。​最頻値は、名義尺度のデータ（血液型、性別など）に適しています。

散布度の指標とその解釈

散布度とは、データのばらつきや広がりを示す指標であり、主に以下の3つが用いられます。

1.範囲（Range）

範囲は、データの最大値と最小値の差であり、データの全体的な広がりを示します。​先ほどの血圧データの場合、範囲は140 - 120 = 20 mmHgとなります。​

範囲は、データのばらつきの大まかな指標として使用されますが、外れ値の影響を受けやすい点に注意が必要です。

2.分散（Variance）

分散は、各データと平均値との差（偏差）の二乗の平均であり、データのばらつきの程度を示します。​分散が大きいほど、データのばらつきが大きいことを意味します。

​ただし、分散の単位は元のデータの単位の二乗となるため、解釈が難しい場合があります。

3.標準偏差（Standard Deviation）

標準偏差は、分散の平方根であり、データのばらつきを元のデータと同じ単位で表します。​標準偏差が大きいほど、データのばらつきが大きいことを意味します。

​標準偏差は、データのばらつきを直感的に理解するために広く用いられます。

データの視覚的表現

データの特徴を視覚的に把握するためには、以下のようなグラフが有用です。

ヒストグラム（Histogram）

ヒストグラムは、データの分布を示す棒グラフであり、データの頻度や分布の形状を視覚的に把握することができます。

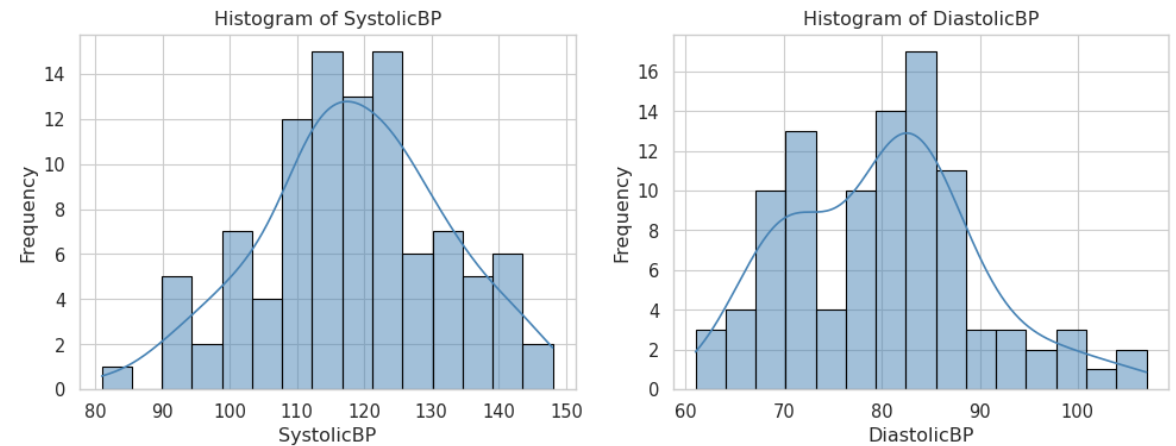
​例えば、患者の血圧データをヒストグラムで表すことで、血圧の分布やピークの位置を確認できます。

 

箱ひげ図（Box Plot）

箱ひげ図（Box Plot）は、データの分布やばらつきを視覚的に表現するためのグラフであり、臨床研究においてもデータの特徴を把握する際に有用です。

 

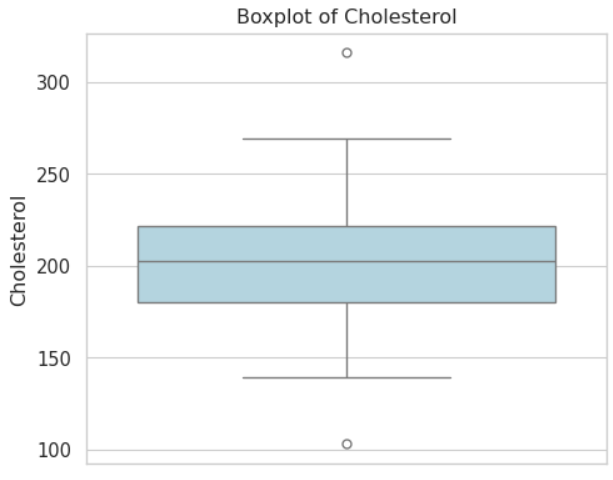
​この図は、データの最小値、第一四分位数（25パーセンタイル）、中央値（50パーセンタイル）、第三四分位数（75パーセンタイル）、最大値の5つの統計量を一目で確認できるように設計されています。

箱ひげ図の構成要素とその解釈

箱（Box）	第一四分位数から第三四分位数までの範囲を示し、データの中央50%がこの範囲内に収まります。箱の中央に引かれた線は中央値を表します。
ひげ（Whisker）	箱の上下から伸びる線で、データの最小値と最大値までを示します。ただし、外れ値が存在する場合、ひげは外れ値を除いた範囲まで伸び、外れ値は個別に表示されます。
外れ値（Outlier）	​他のデータ点から著しく離れた値で、通常は箱ひげ図のひげの外側に点として表示されます。外れ値の定義は、第三四分位数から1.5倍の四分位範囲（IQR）を超える値、または第一四分位数から1.5倍のIQRを下回る値とされます。

 

箱ひげ図の作成方法

箱ひげ図は、統計ソフトウェアや表計算ソフトを使用して作成できます。​例えばExcelでは以下の手順で作成可能です。

• • 1.データを選択します。
  • 2.「挿入」タブの「統計グラフの挿入」から「箱ひげ図」を選択します。
  • 3.生成されたグラフを適宜調整します。

箱ひげ図の利点と注意点

箱ひげ図は、データの中心傾向やばらつきを直感的に把握でき、複数のグループ間での比較も容易です。​しかし、データの分布が非対称である場合や外れ値が多い場合、解釈が難しくなることがあります。

​そのため、他のグラフや統計手法と併用して、データの特徴を総合的に理解することが重要です。

データセットと実装

医療データセットは、臨床現場でよく用いられる3種類の健康指標を模擬したサンプルデータです。以下に各変数の内容とその背景を説明します。

収縮期血圧（SystolicBP）

内容	心臓が収縮して血液を送り出す際に、動脈にかかる最高血圧です。
生成方法	平均120 mmHg、標準偏差15 mmHgの正規分布に従い、100人分のデータを生成しています。
背景	一般的に、収縮期血圧は120 mmHg前後が標準とされ、実際の臨床データでは個人差や測定時の変動が見られます。

 

拡張期血圧（DiastolicBP）

内容	心臓が拡張して血液を受け入れる際に、動脈にかかる最低血圧です。
生成方法	平均80 mmHg、標準偏差10 mmHgの正規分布を利用して、100人分のデータを生成しています。
背景	拡張期血圧は80 mmHg前後が一般的な基準値とされ、収縮期血圧と同様に患者の心血管リスク評価に用いられます。

 

総コレステロール（Cholesterol）

内容	血液中のコレステロール量を示し、心血管疾患のリスク評価に重要な指標です。
生成方法	平均200 mg/dL、標準偏差30 mg/dLの正規分布に従い、100人分のデータを作成しています。
背景	総コレステロール値は、動脈硬化や心臓病のリスク管理において重視される数値であり、個々の健康状態や生活習慣により幅が生じることが特徴 です。

 

Pythonでの使用例

Google colaboでの使用例

＜コードの例＞

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns


# publication-quality用のスタイル設定
sns.set_style("whitegrid")  # Changed from plt.style.use to sns.set_style
sns.set_context("paper", font_scale=1.2)


# 乱数の種を固定
np.random.seed(42)


# サンプルデータ作成：100人分の収縮期血圧（SystolicBP）、拡張期血圧（DiastolicBP）、総コレステロール（Cholesterol）
n = 100
data = pd.DataFrame({
   'SystolicBP': np.random.normal(120, 15, n).round(),
   'DiastolicBP': np.random.normal(80, 10, n).round(),
   'Cholesterol': np.random.normal(200, 30, n).round()
})


# 各変数の散布度（範囲、分散、標準偏差）の計算関数
def compute_dispersion(series):
   data_range = series.max() - series.min()
   data_variance = series.var()
   data_std = series.std()
   return data_range, data_variance, data_std


# 各変数ごとに統計量を計算し表示
stats = {}
for col in data.columns:
   stats[col] = compute_dispersion(data[col])
   print(f"{col}: Range = {stats[col][0]}, Variance = {stats[col][1]:.2f}, Standard Deviation = {stats[col][2]:.2f}")


# ヒストグラムの作成（各変数を個別のサブプロットで表示）
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
for ax, col in zip(axes, data.columns):
   sns.histplot(data[col], kde=True, ax=ax, bins=15, color='steelblue', edgecolor='black')
   ax.set_title(f'Histogram of {col}')
   ax.set_xlabel(col)
   ax.set_ylabel('Frequency')
plt.tight_layout()
plt.show()


# 箱ひげ図の作成（各変数を個別のサブプロットで表示）
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
for ax, col in zip(axes, data.columns):
   sns.boxplot(y=data[col], ax=ax, color='lightblue', fliersize=5, linewidth=1)
   ax.set_title(f'Boxplot of {col}')
   ax.set_ylabel(col)
plt.tight_layout()
plt.show()

 

Rでの使用例

＜posit Cloudでの使用例＞

# 乱数の種を固定（再現性の確保）
set.seed(42)

# 必要なライブラリの読み込み
library(ggplot2)
library(dplyr)
library(tidyr)

# サンプルデータ作成：100人分の収縮期血圧、拡張期血圧、総コレステロール
n <- 100
data <- data.frame(
  SystolicBP = round(rnorm(n, mean = 120, sd = 15)),
  DiastolicBP = round(rnorm(n, mean = 80, sd = 10)),
  Cholesterol = round(rnorm(n, mean = 200, sd = 30))
)

# 各変数の散布度（範囲、分散、標準偏差）の計算
dispersion_stats <- data %>%
  summarise(
    SystolicBP_Range = max(SystolicBP) - min(SystolicBP),
    SystolicBP_Variance = var(SystolicBP),
    SystolicBP_SD = sd(SystolicBP),
    DiastolicBP_Range = max(DiastolicBP) - min(DiastolicBP),
    DiastolicBP_Variance = var(DiastolicBP),
    DiastolicBP_SD = sd(DiastolicBP),
    Cholesterol_Range = max(Cholesterol) - min(Cholesterol),
    Cholesterol_Variance = var(Cholesterol),
    Cholesterol_SD = sd(Cholesterol)
  )
print(dispersion_stats)

# 複数変数の解
data_long <- data %>%
  pivot_longer(cols = everything(), names_to = "Variable", values_to = "Value")

# ヒストグラム：各変数の分布をfaceted plotで表示
p_hist <- ggplot(data_long, aes(x = Value)) +
  geom_histogram(bins = 15, fill = "steelblue", color = "black", alpha = 0.7) +
  facet_wrap(~ Variable, scales = "free") +
  theme_bw(base_size = 14) +
  labs(title = "Histograms of Medical Variables", x = "Value", y = "Frequency")
print(p_hist)

# 箱ひげ図：
p_box <- ggplot(data_long, aes(x = Variable, y = Value)) +
  geom_boxplot(fill = "lightblue", outlier.color = "red", outlier.shape = 16, outlier.size = 2) +
  theme_bw(base_size = 14) +
  labs(title = "Boxplots of Medical Variables", x = "Variable", y = "Value")
print(p_box)

 

まとめ

箱ひげ図は、データの分布やばらつきを視覚的に表現する強力なツールであり、臨床研究においてもデータの特徴を把握する際に有用です。​

正確な解釈と適切な活用により、研究の質を向上させることが期待できます。

 

次回の記事はこちら：医師のための統計学再入門【基礎編】第3回：確率と確率分布の基礎