【応用編】第3回：生存時間解析

臨床研究では、「患者さんが残りどれくらい生存するのか」「いつ合併症が起こるのか」を知りたい場面が多くあります。生存時間解析は、イベント発生までの時間を扱う統計手法で、打ち切りデータを正しく反映しながら生存率やリスク要因を評価できます。

本記事では、無償で利用できる『Veterans’ Lung Cancer』データをPythonで解析しながら、Kaplan–Meier法の基本からCox比例ハザードモデルの理論・実装、さらには検定や注意点までをわかりやすく解説します。

生存時間解析の概要

なぜ生存時間解析を使うの？

通常の解析では「特定のイベントが起こったかどうか」で比較しますが、多くの患者さんは観察期間中にイベントを起こしません。これを「打ち切り（censoring）」と呼びます。

例えば、

• Aさん：6か月後に死亡
• Bさん：12か月まで生存後、フォローアップ離脱
• Cさん：12か月経過時点でイベントなし（観察終了）

という場合、打ち切りを無視すると、生存率が実際より過大または過小に推定される恐れがあります。

生存時間解析では、打ち切り症例も適切に活用しながら生存率を推定できます。

Kaplan–Meier法

解析の流れ

• 1.データ準備：生存期間(time)とイベントの有無(status)を用意する
• 2.モデル適用：KaplanMeierFitter().fit()で生存関数を推定する
• 3.曲線描画：plot_survival_function()で階段状の生存曲線を描く
• 4.群比較：治療群などでフィットを繰り返し、複数曲線を重ねる
• 5.差の検定：ログランク検定 logrank_testで統計的に生存曲線の違いを確認する

ログランク検定とは？

群間の生存曲線が同じかを調べる検定で、p<0.05なら「差がある可能性が高い」と判断します。

データセット紹介

• Veterans’ Lung Cancer（137例）
  転移性肺がん患者の生存日数、イベント有無、治療群、年齢、細胞型など
• ダウンロード先:
  https://raw.githubusercontent.com/vincentarelbundock/Rdatasets/master/csv/survival/veteran.csv

Pythonでの解析

!pip install lifelines
!pip install japanize_matplotlib # 日本語の凡例をつけるためにインストール


import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib # 日本語の凡例をつけるためにインポート
from lifelines import KaplanMeierFitter
from lifelines.statistics import logrank_test


df = pd.read_csv('https://raw.githubusercontent.com/vincentarelbundock/Rdatasets/master/csv/survival/veteran.csv', index_col=0)
kmf = KaplanMeierFitter()


# 全症例
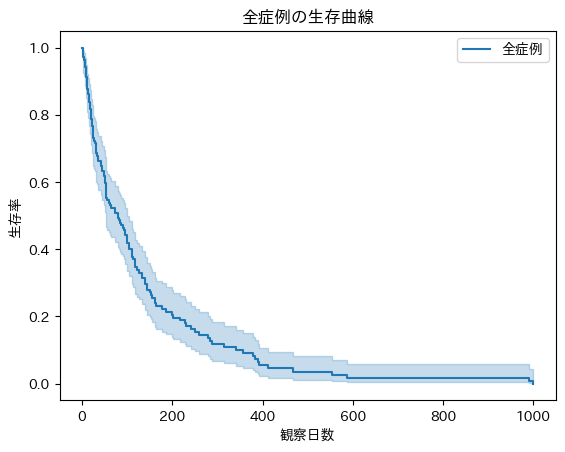
kmf.fit(df['time'], df['status'], label='全症例')
ax = kmf.plot_survival_function()
ax.set(title='全症例の生存曲線', xlabel='観察日数', ylabel='生存率')
plt.show()


# 群別比較
ax = None
for g in [1,2]:
    mask = df['trt']==g
    kmf.fit(df.loc[mask,'time'], df.loc[mask,'status'], label=f'群{g}')
    ax = kmf.plot_survival_function(ax=ax)
ax.set(title='治療群ごとの比較', xlabel='観察日数', ylabel='生存率')
plt.show()


# ログランク検定
res = logrank_test(df[df['trt']==1]['time'], df[df['trt']==2]['time'],
                   event_observed_A=df[df['trt']==1]['status'],
                   event_observed_B=df[df['trt']==2]['status'])
print(f"p値={res.p_value:.3f} -> p<0.05なら差あり")

p値=0.928 -> p<0.05なら差あり

このようにKaplan-Meier曲線が描画され、ログランク検定ではp=0.928という結果になりました。

Kaplan-Meier法を使用する上での注意点・落とし穴

交絡因子の未調整

年齢や併存疾患などが群間で異なると、単純比較だけでは説明できない差が出ます。例として、標準治療群に高齢者が多いと、生存曲線の差が治療効果ではなく年齢差に影響を受けてしまう可能性があります。

多群比較での多重検定

3群以上を比較する場合、複数の組み合わせでp値を評価すると偽陽性（第1種エラー）が増加するため、Bonferroni補正などの調整が必要です。

時刻不明な区間検閲

標準Coxモデルは正確なイベント時刻を前提にするため、3ヶ月ごとの健診などではInterval‐censoredモデルの方が適切な場合があります。

尺度

リスクの比（ハザード比）はモデル全体で解釈し、個別の診断タイミングではなく全期間を通した傾向として理解しましょう。

比例ハザード仮定

Coxモデルは「説明変数が影響するリスク比（ハザード比）が時間が経っても一定である」ということを前提としています。 例えば、ある治療群のリスクが常に対照群の60％のまま維持されるというようなイメージです。

この前提が崩れると、 早期には効果が大きく、後期に効果が小さくなるなど、時間依存性が強い場合に、HRの推定値が実際のリスクを正しく反映しなくなります。

検証方法(後述します)：

• Schoenfeld残差検定：各説明変数の残差と時間の相関を検査し、p値が0.05以上ならHRが時間に依存していないと判断します。
• 累積ハザードプロット：Nelson–Aalen法で累積ハザードを推定し、群別の対数累積ハザード曲線が並行に近いかを視覚的に確認します。

Cox比例ハザードモデル

Kaplan-Meier法による解析のあとは、Coxモデルを使って個別のリスク因子について評価を行います。

モデルの役割

半パラメトリックモデルであるCoxモデルでは、複数要因を同時調整しながら群間差を評価することができ、ハザード比(HR)でリスク要因を定量化できます。

半パラメトリックモデルとは？

基底ハザード（全体の時間経過リスク）は仮定せず、要因効果（HR）だけを推定する手法です。 坂道の傾斜は測らず、2人の歩く速さの比を比べるイメージです。

実装例

from lifelines import CoxPHFitter
# 説明変数処理
df2 = pd.get_dummies(df, columns=['trt','celltype'], drop_first=True)
cph = CoxPHFitter()
cph.fit(df2, duration_col='time', event_col='status')
cph.print_summary()

これを実行すると以下の結果が得られます。3つの表がでてきますので、順番に説明します。

1つ目の表は、モデルの概要です。

• number of events observed＝128：イベント（ここでは死亡など）が観察された件数。137例中128例でイベントが起こっていることを示します。
• partial log-likelihood＝–474.40：部分尤度の対数値。モデルの当てはまりの良さを表し、より大きい（つまり負の値が小さい）ほうが良い適合を示します。

2つ目の表には解析の結果が表示されます。

 

• coef：回帰係数（リスクの対数比）
• exp(coef)：ハザード比（HR）。1より小さいとリスク低下、1より大きいとリスク増加
• se(coef)、coef lower/upper 95%：係数の標準誤差と95％信頼区間
• exp(coef) lower/upper 95%：HRの95％信頼区間

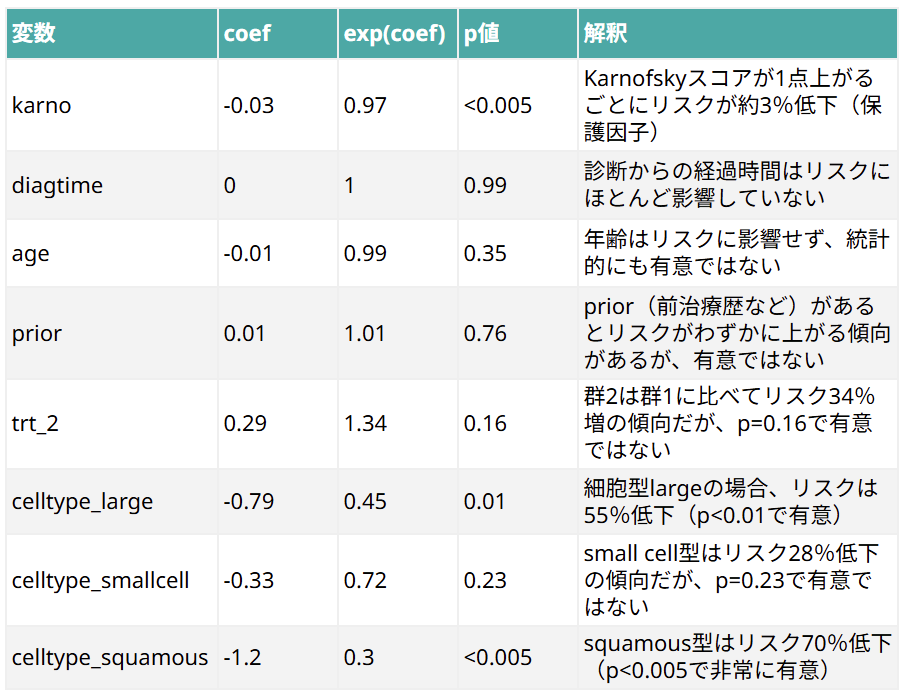
最後に、モデルの適合度について評価した表が得られます。

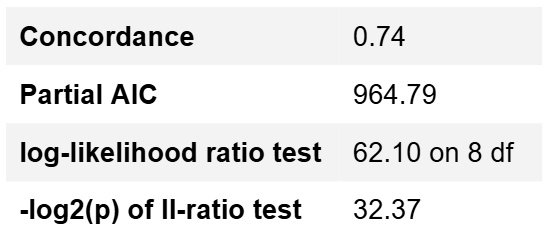
• Concordance＝0.74
  予測確度を示す指標で、0.5（ランダム）～1.0（完全予測）の間をとります。0.74 は比較的良好な識別能力を示します。
• Partial AIC＝964.79
  モデルの情報量基準。AIC は小さいほど良いモデル適合を示します。
• log-likelihood ratio test＝62.10 on 8 df, –log2(p)=32.37
  モデル全体の有意性検定です。自由度8 の下で p が極めて小さい（–log2(p)が32.37）ことから、少なくとも一つ以上の説明変数が有意にリスクと関連していると結論づけられます。

注意点

• 時刻不明な区間検閲：
  標準Coxでは、イベント発生の正確な日時がわかっていることを前提にしているため、3ヶ月ごとの検査でイベント発症を判定するようなケースではInterval‐censoredモデルの方が適切な場合があります。
• 比例ハザード仮定：
  Coxモデルは「ある事象（死亡、再発、故障など）の瞬間的なリスクを表すハザード比が、時間を通じて一定である」という比例ハザード仮定に基づいています。つまり、Coxモデルを使用する場合は時間によるHR変化が小さいことが前提となります。

比例ハザード仮定の検証

以下の方法を用いて、比例ハザード仮定が成立しているかどうかを検証します。

• 1.Schoenfeld残差検定：
  残差と時間の関係でp≥0.05なら仮定が成立します。ただし p値がやや小さい（例：0.02など）場合でも、実務上はグラフの傾向や臨床的妥当性をふまえて慎重に解釈することが勧められています。
• 2.累積ハザードプロット：
  Nelson–Aalen法で推定した対数累積ハザード線が平行に近いかをチェックします

以下のコードで検証を行います。

cph.check_assumptions(df2, show_plots=True)

結果の一部を抜粋します。

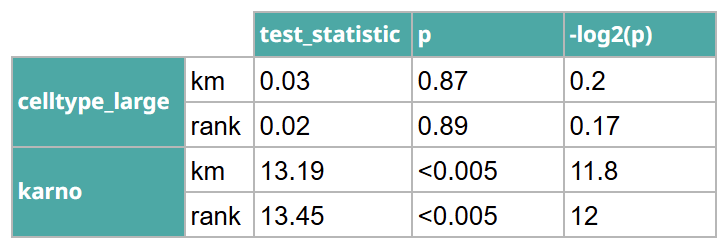
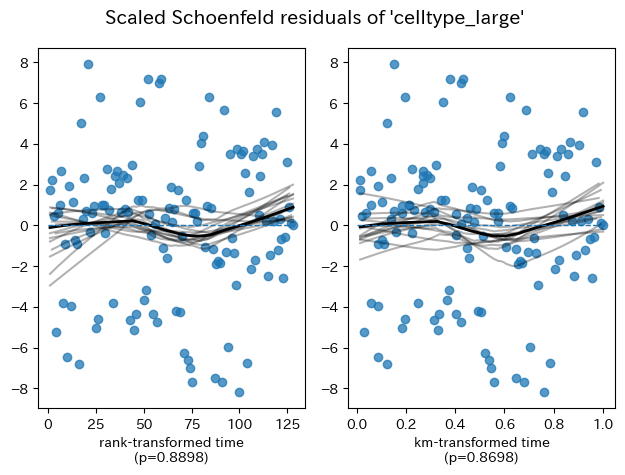
karno（Karnofskyスコア）のp値が非常に小さく（p=0.0002）、比例ハザード仮定に違反しているとみなされます。 celltypeについてはp=0.87と高く、比例ハザード仮定に合致しています。

累積ハザードプロットでは、celltype_largeは水平に近くプロットされていますが、karnoでは右上がりのプロットになっていますね。

まとめ

生存時間解析は、治療効果やリスク要因を時間の流れとともに捉えるという、重要な視点からみた解析方法です。基本的な手法を理解すれば、実臨床での応用がぐっと身近になります。ぜひ身近なデータでも一度試してみてくださいね。