【応用編】第2回：ロジスティック回帰分析

ロジスティック回帰分析の復習

ロジスティック回帰分析は、目的変数が「有病／無病」や「生存／死亡」といった2値のカテゴリカル変数の場合に使用されます。

この分析手法は、アウトカム（目的変数）の発生確率を複数の説明変数（共変量）から予測・説明することを目的としています。特に医学研究では、ある疾患の発症リスクを特定の因子（例えば年齢やBMI、喫煙歴など）から評価する際に頻繁に利用されます。

使用するデータ

今回は、UCI機械学習リポジトリにある「Pima Indians Diabetes Dataset」を使用します。このデータは、768名のピマ・インディアン女性の健康調査から収集されたもので、「糖尿病の有無」をアウトカムとして以下の説明変数が含まれています。

• Pregnancies（妊娠回数）
• Glucose（血糖値）
• BloodPressure（血圧）
• SkinThickness（皮膚厚）
• Insulin（インスリン値）
• BMI（体格指数）
• DiabetesPedigreeFunction（家族歴）
• Age（年齢）

データは以下のURLからダウンロードできます：

https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv

Pythonによるロジスティック回帰分析

はじめに、ヒストグラムを書いてデータをイメージしてみましょう。

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns


# データ読み込み
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv"
columns = ['Pregnancies', 'Glucose', 'BloodPressure', 'SkinThickness', 'Insulin',
           'BMI', 'DiabetesPedigreeFunction', 'Age', 'Outcome']
data = pd.read_csv(url, names=columns)


# ヒストグラム（各変数の分布）
fig, axs = plt.subplots(3, 3, figsize=(15, 12))
axs = axs.ravel()
for i, col in enumerate(data.columns[:-1]):
    sns.histplot(data[col], kde=True, ax=axs[i])
    axs[i].set_title(col)
plt.tight_layout()
plt.show()

 

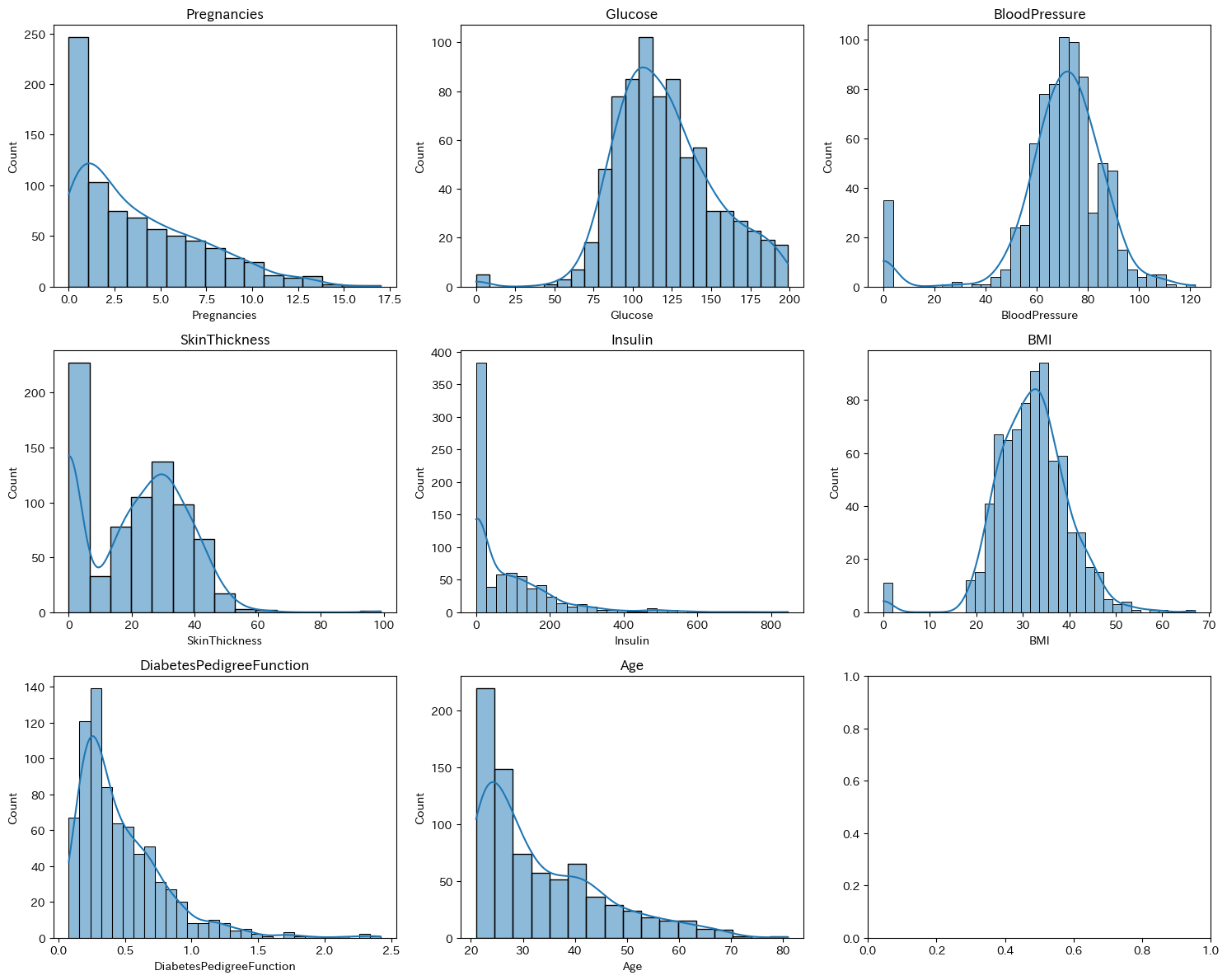
必要に応じて散布図を描画してみるのもよいです。

# 散布図
plt.figure(figsize=(8, 6))
sns.scatterplot(data=data, x='Glucose', y='BMI', hue='Outcome', palette='Set1')
plt.title('Glucose vs BMI by Diabetes Status')
plt.xlabel('Glucose')
plt.ylabel('BMI')
plt.grid(True)
plt.show()

 

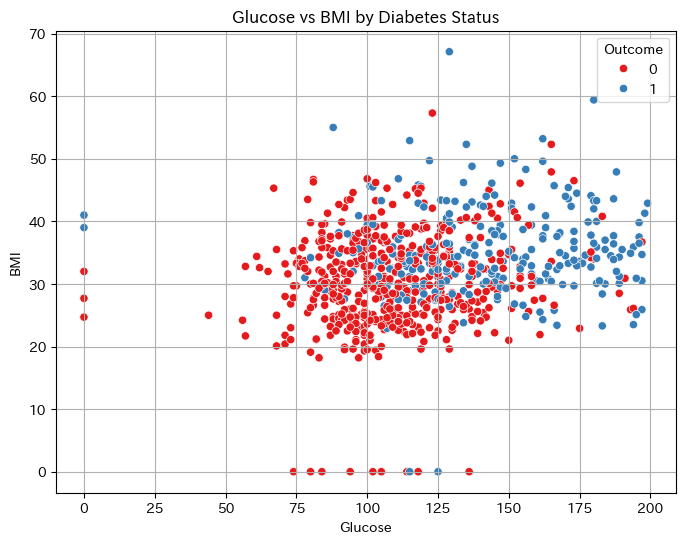
それでは、解析していきましょう。

Pythonでは、pandasとscikit-learnライブラリを用いて解析を進めます。

# ライブラリのインポート
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix
# データ読み込み
data = pd.read_csv("https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv",
                   names=['Pregnancies', 'Glucose', 'BloodPressure', 'SkinThickness', 'Insulin',
                          'BMI', 'DiabetesPedigreeFunction', 'Age', 'Outcome'])
# データ分割
X = data.drop('Outcome', axis=1)
y = data['Outcome']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# モデル構築と学習
model = LogisticRegression(max_iter=1000)
model.fit(X_train, y_train)
# 結果の評価
y_pred = model.predict(X_test)
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))

Pythonによる解析結果の解釈

上のコードを実行すると以下のような結果が得られます。

[[120  31]
 [ 30  50]]
          	precision	recall  f1-score   support
       	0   	0.80      0.79  	0.80   	151
       	1   	0.62      0.62  	0.62    	80
 
accuracy			0.74	231
macro avg	0.71	0.71	0.71	231
weighted avg	0.74	0.74	0.74	231

★予測結果の分類状況（混同行列）

[[120 31], [30 50]] は予測結果の分類状況（混同行列）を表しています。

• 120名は「糖尿病でない」と正しく予測された人（真陰性）
• 50名は「糖尿病あり」と正しく予測された人（真陽性）
• 31名は「糖尿病でない」が誤って「糖尿病あり」と予測された人（偽陽性）
• 30名は「糖尿病あり」だが誤って「糖尿病でない」と予測された人（偽陰性）

★Precision（適合率）

陽性と判定された人のうち、どれだけ正しかったか。たとえば糖尿病ありと判定された80人中、実際に正しかったのは50人 → precision = 50 / (50+31) ≈ 0.62

★Recall（再現率）

実際に糖尿病であった人のうち、どれだけ見逃さずに予測できたか。→ 50 / (50+30) = 0.62

★F1スコア

PrecisionとRecallのバランスを示す指標です。

★Accuracy（正解率）

全体の中で正しく分類された割合。→ (120 + 50) / 231 ≈ 0.74

これにより、モデルは糖尿病の有無をある程度の精度で予測できていることがわかります。

実際のモデルがどのようになっているかを見るには、以下のコードを実行します。

# モデルの係数と切片を出力
coef = model.coef_[0]  # 説明変数の係数（配列）
intercept = model.intercept_[0]  # 切片


# 説明変数名とともに表示
for name, c in zip(X.columns, coef):
    print(f'{name}: {c:.3f}')
print(f'切片: {intercept:.3f}')

すると、次の結果が得られます。

Pregnancies: 0.058
Glucose: 0.036
BloodPressure: -0.011
SkinThickness: -0.001
Insulin: -0.001
BMI: 0.109
DiabetesPedigreeFunction: 0.374
Age: 0.036
切片: -9.431

つまり、このロジスティック回帰分析のモデルは、糖尿病の発症確率 p を用いて、以下のような対数オッズの式（logit式）で表されます。

$$\log\left( \frac{P}{1-P} \right)=-9.431+0.058・Pregnancies+0.036・Glucose-0.011・BloodPressure-0.001・SkinThickness-0.001・Insulin+0.109・BMI+0.374・DiabetesPedigreeFunction+0.036・Age$$

この式は「各変数が1単位増えるごとに、糖尿病になるオッズがどれだけ変わるか」を表しています。

このlogit式を変換して、最終的な糖尿病発症確率 p を求めます。

\(p=\left( \frac{1}{1+e^{-z}} \right)\)　\(ただし\)　\(z=上記のlogit式\)

たとえば、次のような特徴の患者さんがいたとすると、

• 妊娠回数 = 3
• 血糖値 = 130
• 血圧 = 70
• 皮膚厚 = 20
• インスリン = 85
• BMI = 30
• 家族歴 = 0.5
• 年齢 = 40

計算式より、糖尿病を発症している確率 p はおよそ 36.5% となります。

また、混同行列は次のように描画できます。こちらの方が視覚的でわかりやすいですね。

!pip install japanize_matplotlib # 日本語の凡例をつけるためにインストール

import japanize_matplotlib # Import japanize_matplotlib
from sklearn.metrics import ConfusionMatrixDisplay 
# 予測
y_pred = model.predict(X_test)
# 混同行列のプロット
ConfusionMatrixDisplay.from_estimator(model, X_test, y_test, display_labels=['陰性', '陽性'], cmap='Blues')
plt.title('混同行列（Confusion Matrix）')
plt.show()

 

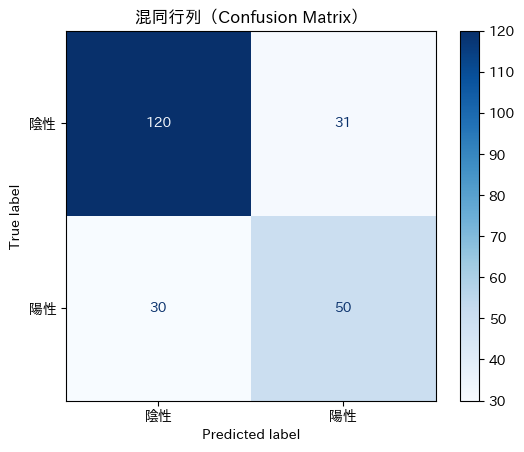
Rによるロジスティック回帰分析

次にRでの実行例を示します。

# ライブラリの読み込み
library(tidyverse)
library(caret)
# データ読み込み
data <- read_csv("https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv", col_names = c('Pregnancies', 'Glucose', 'BloodPressure', 'SkinThickness', 'Insulin', 'BMI', 'DiabetesPedigreeFunction', 'Age', 'Outcome'))
# データ分割
set.seed(42)
train_index <- createDataPartition(data$Outcome, p = 0.7, list = FALSE)
train_data <- data[train_index, ]
test_data <- data[-train_index, ] 
# モデル構築と学習
model <- glm(Outcome ~ ., data = train_data, family = binomial)
summary(model) 
# 予測結果の評価
predicted_probs <- predict(model, test_data, type = "response")
predicted_classes <- ifelse(predicted_probs > 0.5, 1, 0)
confusionMatrix(as.factor(predicted_classes), as.factor(test_data$Outcome))

Rによる解析結果の解釈

Rの出力結果から回帰係数の推定値とそれらの統計的有意性（p値）が確認できます。オッズ比を算出するには、回帰係数を指数変換（exp関数）します。

exp(coef(model))

この出力から、例えばGlucoseの係数が1.05と表示されれば、血糖値が1単位増加するごとに糖尿病のオッズが約5％増加することを示します。

オッズ比と信頼区間の解釈

ロジスティック回帰分析で得られるオッズ比は、ある因子に曝露した群でのイベントのオッズが非曝露群に対して何倍になるかを示します。

例えば、「喫煙者が肺がんを発症する確率」が「非喫煙者と比べて2倍」なら、喫煙者のオッズ比は2ということになります。オッズ比1はリスク不変、1より大きければリスク増加、1未満であればリスク減少を意味します。

また、95%信頼区間（CI）が1をまたがない場合、その因子の影響は統計的に有意であると判断できます。例えば、「BMIのオッズ比が1.2、95%CIが1.05–1.38」であれば、BMIが1単位増えるごとに糖尿病になるオッズが20％増えると解釈します。

結果の評価とモデル改善

モデルの精度はAUC（Area Under the Curve）やROC曲線で評価します。ROC曲線は偽陽性率（横軸）と真陽性率（縦軸）をプロットし、曲線下面積（AUC）が1に近いほど良い予測性能を示します。

PythonでROC曲線を描画してみましょう。

!pip install japanize_matplotlib # 日本語の凡例をつけるためにインストール

from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib.pyplot as plt 
# 予測確率の取得
y_pred_proba = model.predict_proba(X_test)[::,1]
fpr, tpr, _ = roc_curve(y_test, y_pred_proba)
auc = roc_auc_score(y_test, y_pred_proba) 
# ROC曲線のプロット
plt.plot(fpr, tpr, label="AUC = {:.2f}".format(auc))
plt.xlabel("偽陽性率")
plt.ylabel("真陽性率")
plt.title("ROC曲線")
plt.legend(loc=4)
plt.show()

 

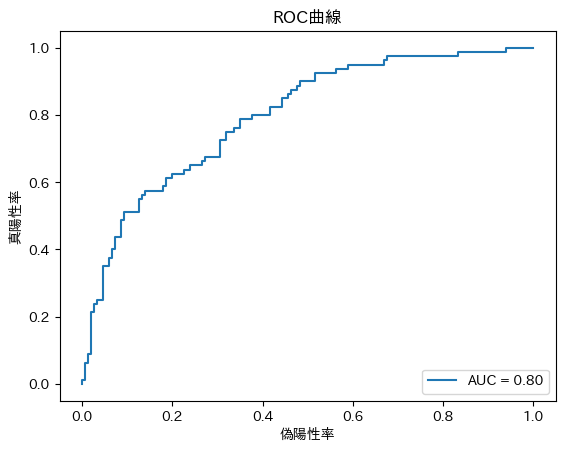
まとめ

ロジスティック回帰分析を用いることで、複数の要因を考慮しながら疾患リスクを定量的に評価できます。オッズ比とその信頼区間を適切に解釈し、結果を臨床的に応用することが重要です。

PythonやRといった統計ソフトを使いこなすことで、実際の研究や臨床に役立てることが可能となります。

次回は、生存時間解析について学んでいきます。